Siły w linach cumowniczych

W Pionie Naukowo-Badawczym została wykonana praca badawcza dotycząca sił w łańcuchach cumowniczych.

Łańcuch górnym końcem B przymocowany jest do jednostki cumowanej, a dolnym zakotwiczony jest na dnie, jak na Rys. 1. Zakładamy, że dno na głębokości h jest poziome. Łańcuch spoczywa na dnie na pewnym odcinku x_A. Początek układu znajduje się na końcu części spoczywającej w punkcie A,. Kotwica może przenosić jedynie siły poziome. Dlatego istotne jest, by x_A > 0, tj. by długość spoczywającej części łańcucha nigdy nie spadła do zera podczas kotwiczenia. Łańcuch jest cięgnem ciężkim.

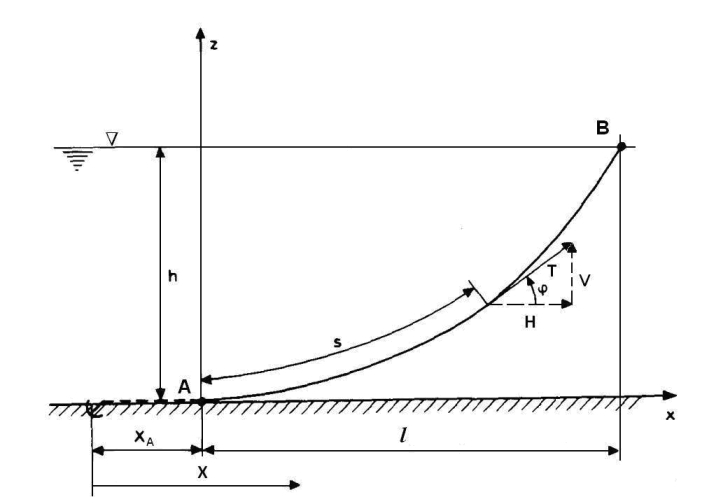
Rys. 1. Symbole użyte do analizy cięgna

Podstawowe zależności

Równaniem linii łańcuchowej przechodzącej przez początek układu jest krzywa łańcuchowa, dana wzorem:

                        z = m(coshx/m - 1),

gdzie m º H/q, H jest składową poziomą naciągu łańcucha, stałą wzdłuż zwisającego łańcucha, zaś q jest jednostkowym ciężarem łańcucha, z uwzględnieniem wyporu. Zadając współrzędne punktu B(l, h), otrzymamy równanie na nieznany parametr m:

                        h = m(coshl/m - 1).

Pozioma długość części zwisającej łańcucha l jest zwykle 5¸20 razy większa od głębokości h.

W analizie łańcucha, wygodnie jest stosować wielkości bezwymiarowe, odniesione do stałej głębokości akwenu h, która jest znana. Wprowadzając oznaczenia: u º m/h, v º l/h, otrzymamy równanie na bezwymiarowy naciąg łańcucha u = m/h º H/qh:

    1/u = coshv/u -1                                                                                              (1)

Z równania wynika, że bezwymiarowy naciąg u jest funkcją zmiennej v = l/h, pokazaną na Rys. 2 linią ciągłą. Kółkami zaznaczona jest aproksymacja kwadratowa tej funkcji: u = ½v². Widać, że w kategoriach absolutnych jest dobra w całym zakresie l/h.

Wzór (1) pozwala łatwo wyznaczyć składową poziomą napięcia cięgna H, gdy znamy głębokość h, stosunek l/h = v i masę jednostkową łańcucha r. Przykładowo, gdy v º l/h = 10, otrzymamy, że m/h º H/qh = ½10² = 50. Stąd, składowa pozioma napięcia H = 50qh. Na akwenie o głębokości h = 150 m i masie jednostkowej łańcucha r = 150 kg/m, pozioma składowa napięcia wynosi H = 11036 kN. Gdyby l/h = 5, składowa H byłaby 4 razy mniejsza.

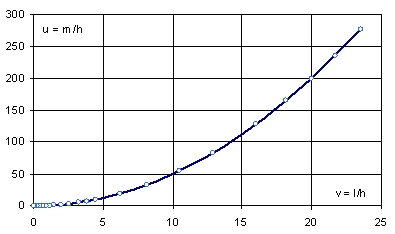
Rys. 2. Zależność parametru u º m/h = H/qh od zmiennej v = l/h

Znając parametry m i l, długość zwisającej części łańcucha dana jest wzorem: s = msinhl/m, lub w formie bezwymiarowej: s/h = usinhv/u. Funkcja ta przedstawiona jest na Rys. 3.

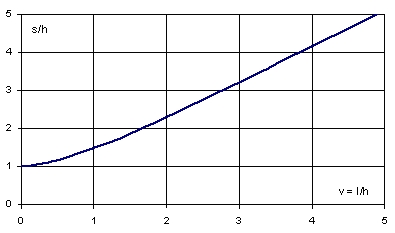
Rys. 3. Zależność bezwymiarowej długości liny s/h od zmiennej v = l/h

Nachylenie łańcucha w dowolnym punkcie dane jest wzorem: tgj = s/m = sinhx/m. Maksymalne nachylenie na końcu łańcucha w punkcie B wynosi: tgj = sinhl/m.

Napięcie łańcucha T w dowolnym punkcie określa wzór: T = q(m + z). W punkcie B na końcu łańcucha, napięcie wynosi: T = q(m + h), lub w formie bezwymiarowej: T/qh = 1 + u.

Z Rys. 2 widać, że zmiana poziomej długości zwisającego łańcucha, np. wywołana ruchami statku, skutkuje zmianą składowej poziomej napięcia i kształtu zwisającego łańcucha (Rys. 4).

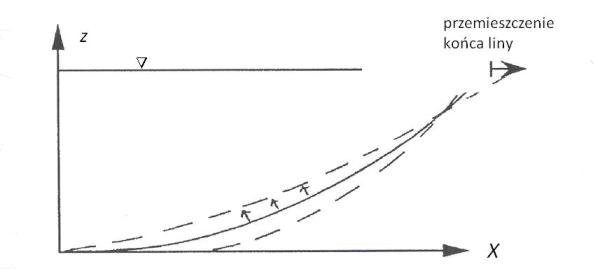   Rys. 4. Zmiana kształtu cięgna wywołana przemieszczaniem końca

Sztywność napięcia łańcucha

Pochodna dH/dl = qv = 2H/l, gdzie v º l/h, jest współczynnikiem sztywności łańcucha. Im większy jest ciężar jednostkowy łańcucha q i stosunek l/h, tym sztywniejsze jest napięcie łańcucha.

W zastosowaniach potrzebna jest sztywność napięcia łańcucha względem przemieszczenia statku dX, czyli względem przemieszczenia punktu B na końcu łańcucha. Dana jest ona wzorem:

                        dH/dX = 1,5v³q.

Wzór powyższy, ściśle rzecz biorąc, ważny jest dla małych przemieszczeń łańcucha w punkcie B. Dla skończonych przemieszczeń DX zmiana poziomego napięcia łańcucha DH wyraża się wzorem:

                        DH = 1,5v₀³(1 + e)(1 + ½e)qDX,

gdzie v₀ º l₀/h jest początkową wartością stosunku l/h, e = Dl/l₀ º Dv/v₀ jest względną zmianą długości liny, równą: e = 1,5vDX/h. Dzieląc powyższy wzór przez qh, otrzymamy postać bezwymiarową:

                        Du = 1,5v₀³(1 + e)(1 + ½e)DX/h.

Wykres tej wielkości w funkcji względnego przemieszczenia końca liny DX/h przedstawiony jest na Rys. 5 dla trzech wartości stosunku v = l/h = 3, 3,5, 4.

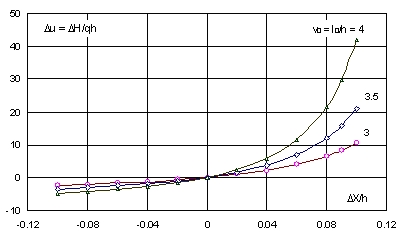
Rys. 5. Wpływ przemieszczenia końca łańcucha na zmianę siły przywracającej

Widać, że siła przywracająca H zmienia się nieliniowo zwłaszcza, gdy koniec liny oddala się od zakotwiczenia, przy czym nieliniowość wzrasta ze wzrostem stosunku v º l/h. Pochodna w zerze (Du)' = 1,5v₀³. Iloczyn

                                          (1 + e)(1 + ½e) = Du/Du_l

przedstawia wpływ nieliniowości na sztywność łańcucha. Wykres Du/Du_l = (1 + e)(1 + ½e) w funkcji względnego przemieszczenia końca liny DX/h przedstawiony jest na Rys. 6 dla trzech wartości stosunku v = l/h = 3, 3,5, 4. Gdyby zmiana siły przywracającej była liniowa, tj. proporcjonalna do przemieszczenia, stosunek Du/Du_l byłby równy 1. Z wykresu widać, że gdy przemieszczenie DX = 8%h, to przyrost siły przywracającej dla v = l/h = 3 jest dwukrotnie większy, niż to by wynikało z teorii liniowej, a dla l/h = 4 prawie trzykrotnie. Pochodna w zerze (Du/Du_l)' = 2,25v_. Styczna o tym współczynniku pokazana jest na Rys. 6 linią przerywaną dla v₀ = 3.

Względny przyrost siły przywracającej Du/u_ º DH/H_ dany jest wzorem: Du/u₀ = 3v₀(1 + e)(1 + ½e)DX/h. Widzimy, że jest on proporcjonalny do v₀ = l₀/h. Zatem, dzieląc Du/u₀ przez v₀, otrzymamy:

                                Du/u₀v₀ = 3(1 + e)(1 + ½e)DX/h.

Wykres tej wielkości w funkcji względnego przemieszczenia końca liny DX/h przedstawiony jest na Rys. 7. Są to krzywe dość silnie wygięte zwłaszcza, gdy DX > 0 Pochodna w zerze (Du/u₀v₀)' = 3, jest stała, niezależna od v_. Oznacza to, ze w sąsiedztwie zera wszystkie krzywe mają wspólny przebieg.

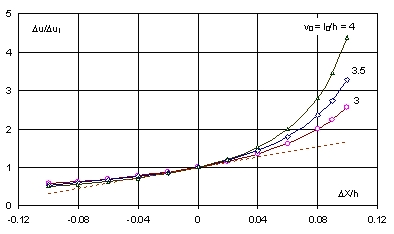
Rys. 6. Nieliniowość sztywności łańcucha

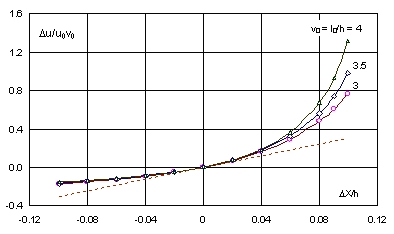Rys. 7

Gdyby sztywność liny była stała, wówczas Du/u_v_ = 3DX/h; wykresem tej wielkości byłaby linia prosta o współczynniku kierunkowym 3, pokazana linią przerywaną na Rys. 7. Jest ona styczna do krzywych w początku układu. Widać, że nieliniowość sztywności liny można zaniedbać, gdy przemieszczenia końca liny DX w płaszczyźnie poziomej nie przekraczają ±0,04h, czyli gdy nie przekraczają 4% głębokości akwenu h.

Analogiczne zależności można otrzymać z rozważań energetycznych.

Działające siły

Na zacumowany obiekt mogą działać siły od:

• wiatru
• i lodu.

• prądu
• falowania

Cumy dobiera się na ekstremalne warunki, jakie mogą wystąpić w okresie 100 lat. Dla Morza Północnego stuletnia średnia prędkość wiatru na wysokości h = 10 m n.p.m. wynosi u = 41 m/s, czyli 148 km/h.

Przyjmuje się, że w okresie 20-25 lat eksploatacji statek napotyka na 10⁸ fal. Zatem, w okresie 100 lat daje to około 4,5×10⁸ = 10^8,7 oscylacji.

Dla typowego okresu eksploatacji statku 20-25 lat szukamy poziomu odpowiedzi statku przekraczanego z prawdopodobieństwem P_a = 10^-8, czyli średnio raz w okresie eksploatacji statku, a w wypadku obiektów oceanotechnicznych – poziomu przekraczanego z prawdopodobieństwem P_a = 10^-8,7, czyli średnio raz na 100 lat. W tym ostatnim przypadku możemy mówić o amplitudzie stuletniej.

Napór falowania

Napór wywołany falowaniem najprościej jest oszacować metodą Gerritsmy–Beukelmana na obliczanie przyrostu oporu na fali regularnej. Jest ona ważna także dla statku zacumowanego, dany wzorem:

                        R_AW = (wkò_Lb₃₃Y_w²dx)½z₀².

Wyrażenie w nawiasie ma wymiar kg/ms², identyczny jak iloczyn ciężaru właściwego i długości. Wyciągając przed nawias gB²/L, gdzie g = rg jest ciężarem właściwym wody, zaś B i L to wymiary główne statku, otrzymamy bezwymiarowy współczynnik dodatkowego oporu na fali regularnej r_AW, zależny od częstości fali w, a niezależny od amplitudy fali:

                        r_AW = (kwò_Lb₃₃Y_w²dx)/g(B²/L).

Z pomocą tego współczynnika, przyrost oporu wyrazi się wzorem:

                        R_AW = r_AWg(B²/L)½z₀²,

Przejście na falę nieregularną jest proste. Uwzględniając, że ½z₀² = S(w)dw, stąd,

                        R_AW = g(B²/L)òr_AWS(w)dw.

Napór falowania można więc obliczyć teoretycznie, w oparciu o znajomość współczynnika tłumienia dla nurzań b₃₃ dla przekrojów wręgowych i funkcji przenoszenia ruchów względnych wręgu Y_w. Bezwymiarowy współczynnik przyrostu oporu na fali regularnej r_AW można znaleźć też za pomocą badań modelowych oporu okrętu na fali regularnej, w oparciu o wzór: r_AW º R_AW/g(B²/L)½z₀².

Do celów szacunkowych dogodny jest przedostatni wzór, gdzie r_AW jest średnim bezwymiarowym współczynnikiem dodatkowego oporu na fali nieregularnej, a ½z₀² zastąpione jest wariancją m₀ = (¼H_s)² dla najwyższego stanu morza. Dla Morza Północnego H_s = 13,5 m. Można przyjąć wstępnie, że r_AW » 2.

Siła wywołana prądem

Siłę tę obliczamy tak, jak dla statku na wodzie spokojnej poruszającego się z prędkością, jak prąd. Ze względu na stosunkowo niewielkie prędkości prądu siła ta redukuje się do oporu lepkości, danego wzorem:

                        R_cx = c_Fr½u²W,

gdzie r jest gęstością wody w kg/m³, u jest prędkością prądu w m/s, W jest powierzchnią zwilżoną kadłuba w m², zaś c_F jest współczynnikiem tarcia płaskiej płyty:

                        c_F = 0,075/(lgRe – 2)²,

gdzie Re = uL/n jest liczbą Reynoldsa, L jest długością statku w m, zaś n jest kinematycznym współczynnikiem lepkości wody w m²/s. W wypadku ukośnego ustawienia statku względem kierunku prądu, bierzemy składową podłużną prędkości.

Przy poprzecznym ustawieniu statku względem prądu, siła oporu dana jest wzorem:

                        R_cy = c_D½ru²LT,

gdzie T jest średnim zanurzeniem statku, zaś c_D » 0,6 jest współczynnikiem oporu.

Siła wywołana wiatrem

Siła ta równa się oporowi powietrza, jaki działa na nadwodną część statku. Wzór na opór powietrza przyjmuje następującą postać:

                        R_A = c_A½r_Au_A²A_T,

gdzie r jest gęstością wody w kg/m³, u_A jest prędkością wiatru w m/s, A_T jest powierzchnią rzutu wręgowego nadwodnej części kadłuba w m², zaś c_A » 0,6 jest współczynnikiem oporu powietrza.